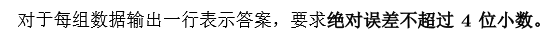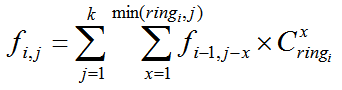开锁
Time Limit: 10 Sec Memory Limit: 256 MB
Description
A君有n个盒子,每个盒子被一把锁锁着,每个盒子内都有一把钥匙。
对于每个盒子而言有且仅有一把钥匙能打开锁着它的锁,而打开它后便能拿着放置在这个盒子内的钥匙去开启其他盒子。
现在A君打算随机选择k个盒子并用魔法将它们打开,并用所得到的钥匙去尝试开启其他所有的盒子(开启一个盒子后,新得到的钥匙还能继续尝试使用)。
A君想知道:最终他能打开所有盒子的概率是多少,请你帮助他。

Output

4
5 1
2 5 4 3 1
5 2
2 5 4 3 1
5 3
2 5 4 3 1
5 4
2 5 4 3 1
Sample Output
0.000000000
0.600000000
0.900000000
1.000000000
HINT

Main idea
一个宝箱内有一个可以开启别的宝箱的钥匙,可以选择k个宝箱,询问能开启所有宝箱的概率。
Solution
我们一看就知道这是一道概率DP的题目。
我们发现,每个宝箱有一个对应的钥匙,那么显然若干个宝箱会构成一个环,只要开了一个环中的一个宝箱就可以开启这个环。
那么我们要求的就是:在n个数中选k次,已知每个环的大小,选中环中的一个元素即视为选中了这个环,问每个环都被至少选了一次的概率。
显然直接记概率不好计算,于是我们可以算出可行的方案数。
我们先求出每个环的大小,然后令 f[i][j] 表示前 i 个环选了 j 个元素的方案数,那么显然可以枚举这一个环中选了几个,那么显然有:

然后我们最后用 f[num][k] / 总方案数 C(n,k) 即可。注意要用double来存,否则数字不够大。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
| #include<bits/stdc++.h>
using namespace std;
const int ONE=310;
int T,n,k;
int a[ONE],vis[ONE],cnt;
int ring[ONE],num;
int record;
double C[ONE][ONE];
double f[ONE][ONE];
int get()
{
int res=1,Q=1;char c;
while( (c=getchar())<48 || c>57 )
if(c=='-')Q=-1;
res=c-48;
while( (c=getchar())>=48 && c<=57 )
res=res*10+c-48;
return res*Q;
}
void Solve()
{
n=get(); k=get();
for(int i=1;i<=n;i++) a[i]=get(),vis[i]=0;
num=0;
for(int i=1;i<=n;i++)
{
if(vis[i]) continue;
int x=i;
cnt=0;
for(;;)
{
vis[x]=1; x=a[x]; cnt++;
if(x==i) break;
}
ring[++num]=cnt;
}
memset(f,0,sizeof(f));
f[0][0]=1; record=0;
for(int i=1;i<=num;i++)
{
record+=ring[i];
for(int j=1;j<=record;j++)
{
for(int x=1;x<=ring[i] && x<=j;x++)
{
f[i][j] += f[i-1][j-x] * C[ring[i]][x];
}
}
}
cout<<(double)f[num][k]/C[n][k]<<endl;
}
int main()
{
C[0][0]=1;
for(int i=1;i<=300;i++)
{
C[i][0]=1;
for(int j=1;j<=300;j++)
C[i][j]=C[i-1][j-1]+C[i-1][j];
}
T=get();
while(T--)
Solve();
}
|